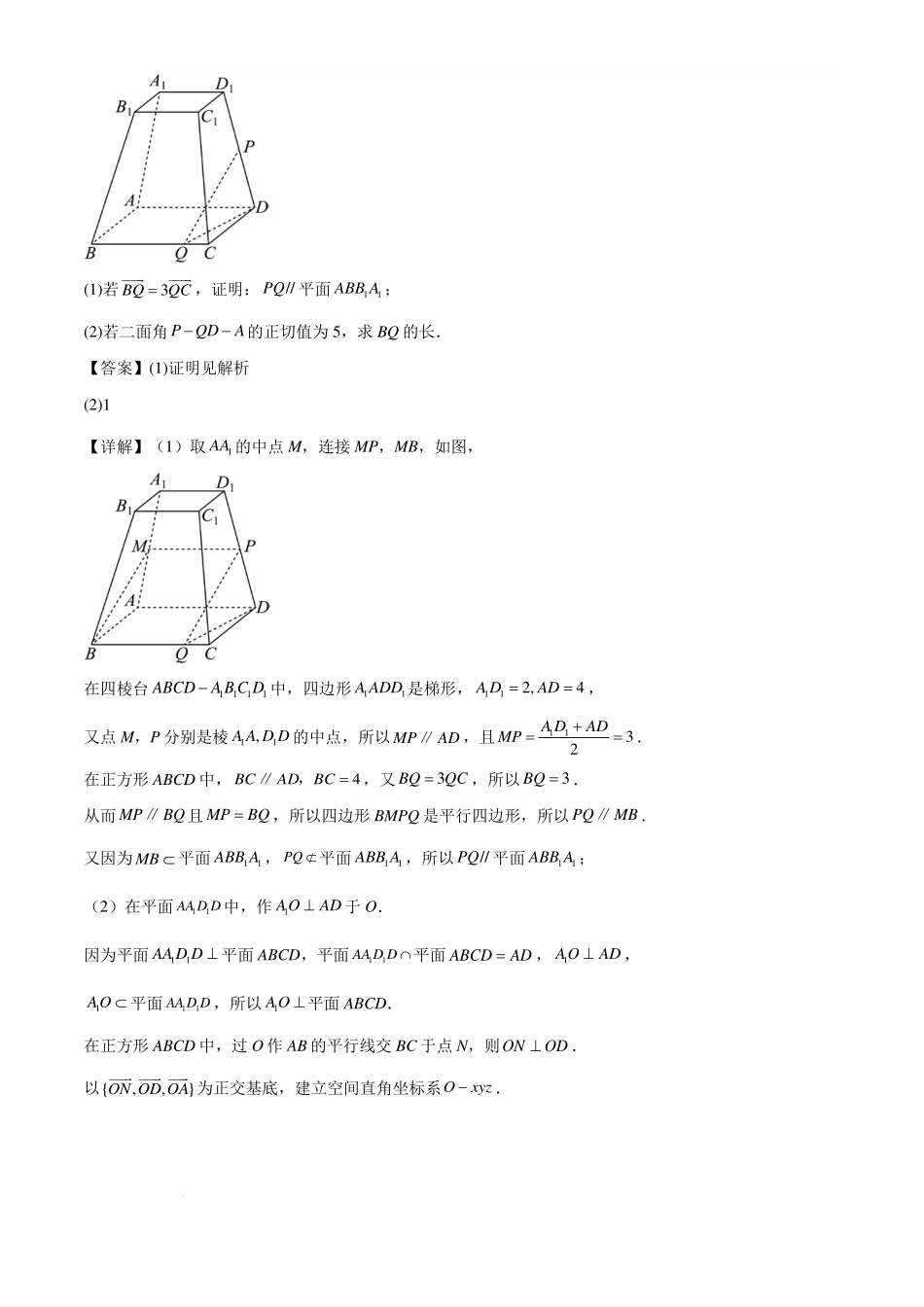
学科网(北京)股份有限公司 学科网(北京)股份有限公司 2025 届新高三暑期效果联合测评答案 选择题: 题号 1 2 3 4 5 6 7 8 9 10 11 答案 D C A D C C D B CD ABD AC 填空题: 12. 1136 13 33 3+ 14. 5 解答题: 15.(本小题 13 分) 已知正项数列{ }na中,113a =,且()22*11320nnnnaaaan+++−=∈N. (1)求数列{ }na的通项公式; (2)()*1111nnnnnnnaabna aaa+++−=∈+++N,证明:1214nbbb++⋅⋅⋅+<. 【答案】(1)13nna =,*n∈N ; (2)证明见解析 【详解】(1)由()()2211113230nnnnnnnnaaaaaaaa+++++−=+−=,0na >, 得113nnaa+ =,又113a =, 则{ }na是以 13 为首项, 13 为公比的等比数列, 所以13nna =,*n∈N . (2)证明:因为1111nnnnnnnaaba aaa+++−=+++ () ()()()()1*1111111111nnnnnnaanaaaa++++−+==−∈++++N, 所以12nbbb++⋅⋅⋅+ 111111111133111111144413nkkknnaaaa=+++=−=−=−< −=+++++∑. 16.(本小题 15 分) 已知函数( )2lnf xxaxax=−+. 学科网(北京)股份有限公司 学科网(北京)股份有限公司 (1)当2a =时,求曲线( )yf x=在点( )()1,1f处的切线方程. (2)若函数 ( )( )g xf xax=−有两个零点,求实数a 的取值范围. 【答案】(1)10xy+− = (2)10, 2e 【详解】(1)当2a =时,( )2ln22f xxxx=−+,所以( )142fxxx −′=+, ( )11 421f= −+= −′,( )1ln1 220f=−+=, 所以曲线( )yf x=在点( )()1,1f处的切线方程为()1yx= −−, 即10xy+− =; (2) ( )( )()2ln0g xf xaxxaxx=−=−>, 由 ( )0g x =得2lnxax=, 2ln,==xya yx的图象有 2 个交点, 令 ( )()2ln0xh xxx=>, ( )31 2lnxh xx−′=,当0ex<<时,( )0h x′>, ( )h x 单调递增, 当ex >时,( )0h x′<, ( )h x 单调递减,所以 ( )()1e2eh xh≤=, 且1x > 时, ( )0h x >, ( )10h=, 所以01x<< 时, ( )0h x <,所以 ( )h x 的大致图象如下, 所以若函数 ( )( )g xf xax=−有两个零点, 则102ea<<, 所以实数a 的取值范围为10, 2e. 17.(本小题 15 分) 如图,已知四棱台1111ABCDA B C D−的上、下底面分别是边长为 2 和 4 的正方形,平面11AA D D ⊥ 平面ABCD,1117A AD D==,点 P 是棱1DD 的中点,点 Q 在棱 BC 上. 学科网(北京)股份有限公司 学科网(北京)股份有限公司 (1)若3BQQC=,证明://PQ平面11ABB A ; (2)若二面角 PQDA−−的正切值为 5,求 BQ 的长. 【答案】(1)证明见解析 (2)1 【详解】(1)取1AA 的中点 M,连接 MP,MB,如图, 在四棱台1111ABCDA B C D−中,四边形11A ADD 是梯形,112,4A DAD==, 又点 M,P 分别是棱11,A A D D 的中点,所以 MPAD∥,且1132A DADMP+==. 在正方形 ABCD 中,4BCADBC =∥,,又3BQQC=,所以3BQ =. 从而 MPBQ∥且 MPBQ=,所以四边形 BMPQ 是平行四边形,所以 PQMB∥. 又因为 MB ⊂ 平面11ABB A , PQ ⊂/ 平面11ABB A ,所以//PQ平面11ABB A ; (2)在平面11AA D D中,作1AOAD⊥于 O. 因为平面11AA D D ⊥ 平面 ABCD,平面11AA D D ∩平面 ABCDAD=,1AOAD⊥, 1AO ⊂ 平面11AA D D ,所以1AO ⊥ 平面 ABCD. 在正方形 ABCD 中,过 O 作 AB 的平行线交 BC 于点 N,则ONOD⊥. 以{,,}ON OD OA 为正交基底,建立空间直角坐标系Oxyz−. 学科网(北京)股份有限公司 学科网(北京)股份有限公司 因为四边形11AA D D 是等腰梯形,112,4A DAD==,所以1AO = 又1117A AD D==,所以14AO =. 易得15(4, 1,0),(0,3,0),(4,3,0),(0,2,4),0,,22BDCDP− , 所以1(4,0,0),0,,2 ,(0, 4,0)2DCDPCB==−=−. 设(0, 4 ,0)(01)CQCBλλλ==−≤≤,所以(4...