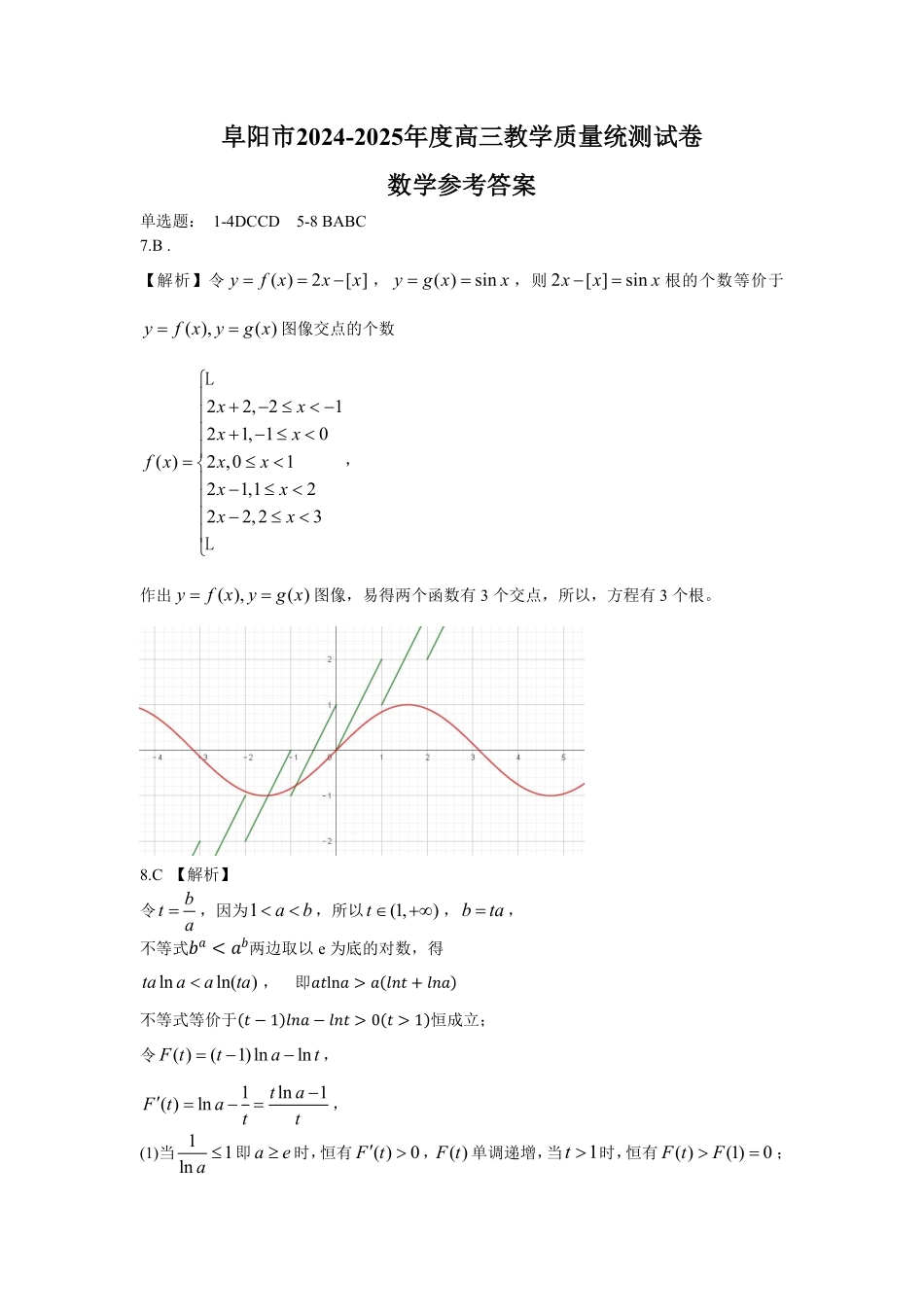
阜阳市2024-2025年度高三教学质量统测试卷数学参考答案单选题: 1-4DCCD5-8 BABC7.B .【解析】令( )2[ ]yf xxx,( )sinyg xx,则 2[ ]sinxxx根的个数等价于( ),( )yf xyg x图像交点的个数22, 2121, 10( )2 ,0121,1222,23xxxxf xxxxxxx LL,作出( ),( )yf xyg x图像,易得两个函数有 3 个交点,所以,方程有 3 个根。8.C 【解析】令bta,因为1ab,所以(1,)t ,bta,不等式 < 两边取以 e 为底的对数,得lnln()taaata,即ln > + 不等式等价于 − 1 − > 0 > 1 恒成立;令( )(1)lnlnF ttat,1ln1( )lntaF tatt,(1)当 11ln a 即 ae时,恒有( )0F t, ( )F t 单调递增,当1t 时,恒有( )(1)0F tF;(2)当11ln a 时,即 1ae时,1(1,)lnta时,有( )0F t,( )F t单调递减,则( )(1)0F tF不合题意,舍;综上, ae.多选填多选题 :9. ABC10.ABD11.ABD10.ABD【解析】2(23)( )(1)xe xxfxx,得函数的递增区间为3(,0),( ,)2 ,递减区间为3(0,1),(1, )2,得 A 错误,B 正确;取134a ,则23( )04af,C 错误;当2x 时,恒有2( )32f xe,则当121322,()2,()2aaf aaf aL1()2nnaf a ,D 正确;11.ABD【解析】因为 P、F 均为球的切点,易得 MF=MP,A 正确;设平面 I 平面 VFO=直线 FG,直线 FG 交 l 于 G,因为 VA// ,所以/ /VAFG ,因为,O Fl,所以lO F,,VOl ,所以lVO,由,VO O F 平面VOF ,所以l 平面VOF ,FG 平面VOF ,所以lFG,又 MN⊥l,所以 MN//FG,因为 FG//VA,所以 MN//VA,B 正确;作 MH 垂直平面 于 H,又因为,VO 所以 MH //VO ,由等角定理可得,∠NMH = ∠AVO' = θ = ∠PMHMH⊥平面 ,得 RT PMHRT NMH,MNMP,又 P、F 均为球的切点,则易得 MF=MP,所以恒有 MN=MF,即|MF|=d,其中 F 为定点,d 为 M 到定直线 l 的距离,所以 M 的轨迹为抛物线,C 错误;圆锥过 VOF 的轴截面,如图所示,取 FG 中点 Q,易得O QVO,22tanFGFQR,在平面 内,若以 Q 为坐标原点,QF 为 x 轴正向,可得方程为2 = 4θ可得该抛物线的开口随着tanR 的增大而增大,D 正确.填空题:12.3 或1313.133614.27415:(1)因为)sin(sin)sin)(sin(ACaBCcb,所以由正弦定理得acbca222,.......2分由余弦定理得212cos222acbcaB,又 B0,....4分所以3B........5分(2) D 为线段 AC 的中点,故12BDBABC,222211244BDBABCBABA BCBC ,因为π3B ,3BD ,故221πs2943cocc aa,整理可得2236acac,...8分在BCA中,由余弦定理得222π2cos 3bacac,所以2212acac,两式联立可得12ac ,所以4 3ac,...12分从而BCA的周长为4 32 36 3abc .16【解析】:(1)取 AB 的中点 G,连接 GF,CG,因为 F 为 BE 中点,所以 FG//EA,FG= 12EA=CD,……(2 分)因为 EA⊥平面 ABC,DC⊥平面 ABC,所以 DC//EA.又因为 FG//EA,所以 DC//FG,所以四边形 CGFD 为平行四边形,所以 DF//CG;……(4 分)因为/DF 平面 ABC,CG 平面 ABC,所以 DF//平面 ABC. ……(6 分)(2)如图所示建立空间直角坐标系,设 AC=m,则(0,2,0),(0,0,2),( ,0,1)BED m,(0, 2,2),( , 2,1)BEBDm,……(8 分)设( , , )x y zn为平面 BDE 的法向量,则有00BEDE nn得22020yzmxyz,……(10 分)令 y=m,得(1,,)m m...